1.1 情報
インターネット上で、「情報」という言葉の意味について調べてみる。
goo辞書
日常生活において「情報」という言葉は、
| (1) 事実やデータ (2) 意思決定に何らかの影響を及ぼす知識 |
など、色々な意味で使われている。「情報」という言葉を厳密に定義するのは難しい。そこで、「情報」という考えを数量化して具体的に取り扱うことを考えてみる。
1.1.1 情報の表現
N進数: N個の数字で数を表現する。例えば10進数の27という数を2進数、16進数で表現してみる。
| 10進数 | 10個の文字(0~9)で数を表現する。 10のべき乗の係数で数を表記する。 (27)10=2×101+7×100 |
| 2進数 | 2個の文字(0, 1)で数を表現する。 2のべき乗の係数で数を表記する。 (11011)2=1×24+1×23+0×22+1×21+1×20 |
| 16進数 | 16個の文字(0~9, A~F)で数を表現する。 Aは10進数で10、Bは11、***、Fは15を意味する。 16のべき乗の係数で数を表記する。 (1b)16=1×161+B×160 |


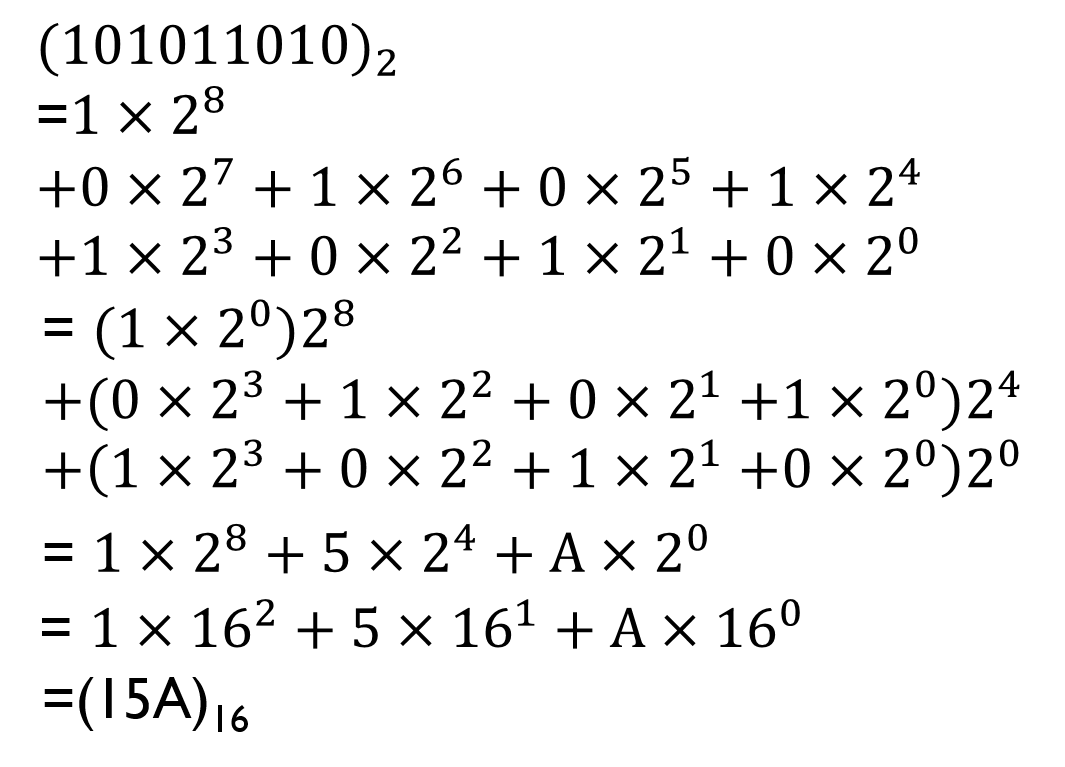
コンピュータに入力される文字、音声、画像といった情報は、2進数で表現される。下図は文字を2進数で表現した例である。この表現は、文字コードと呼ばれる。文字コードは下図の英語を表現するASCIIコード以外にも、様々なものがある
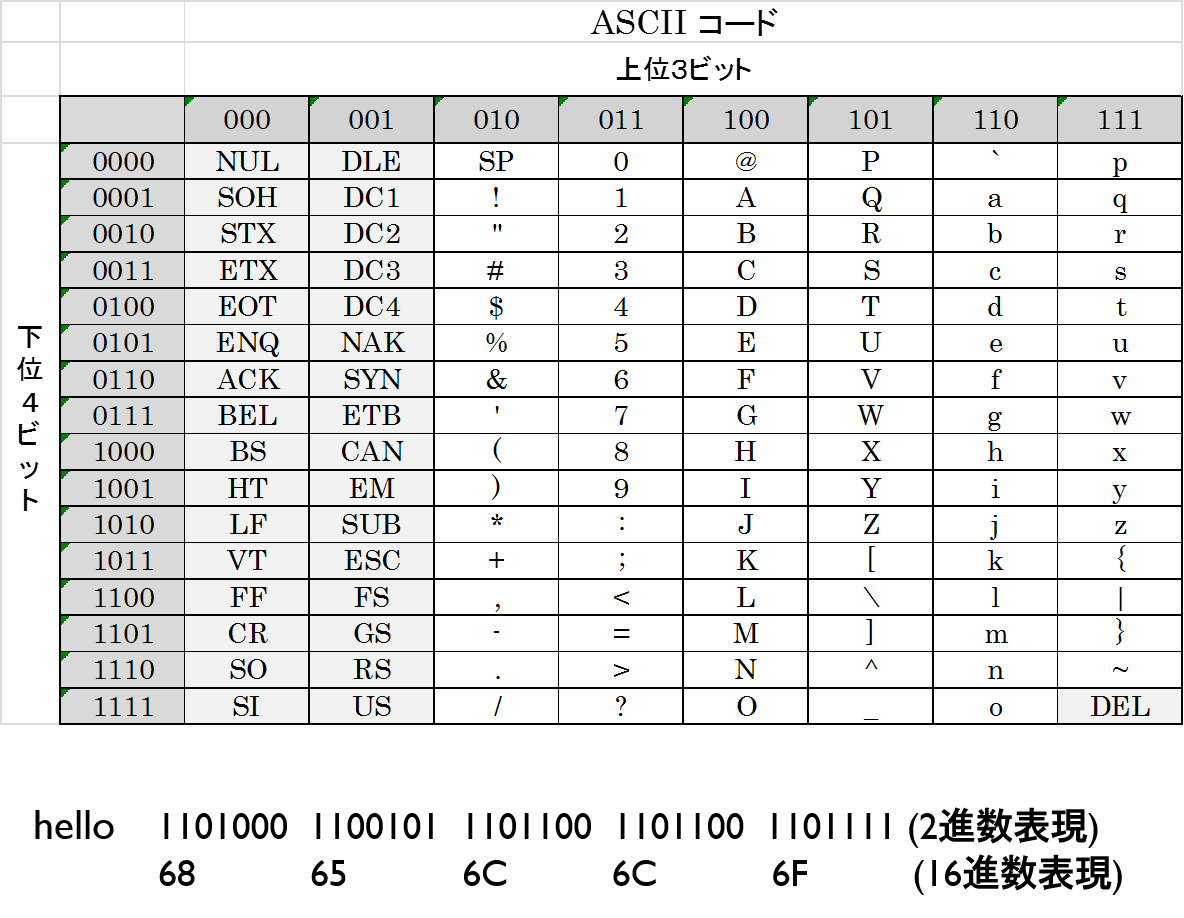 図1
図12進数は桁数が多く分かりづらいので、表記は16進数で行われることが多い。
1.1.2 情報量
「情報」という概念を単純化し、それを数値化して取り扱う情報理論の基礎を確立したのはシャノン(Claude Elwood Shannon)であり、その内容が書かれた論文 A Mathematical Theory of Communication (日本語訳:通信の数学的理論、植松友彦、ちくま学芸文庫)は1948年に出版された。その論文では、情報の大きさを量るものとして情報量を与え、その値から導かれる情報エントロピーという概念が提案された。
以下、情報量について簡単に説明する。まず、2進数、すなわち、1(YES,on),0(NO,off)で、ある事柄(事象)を表現することを考える。現在普及しているデジタルコンピュータは、この方式を使っている。例えば、以下のように、1,0の文字だけを使用して事象を表現する。
| 表・裏(事象が2つ) 1, 0 春・夏・秋・冬(事象が4つ) 00, 01, 10, 11 |
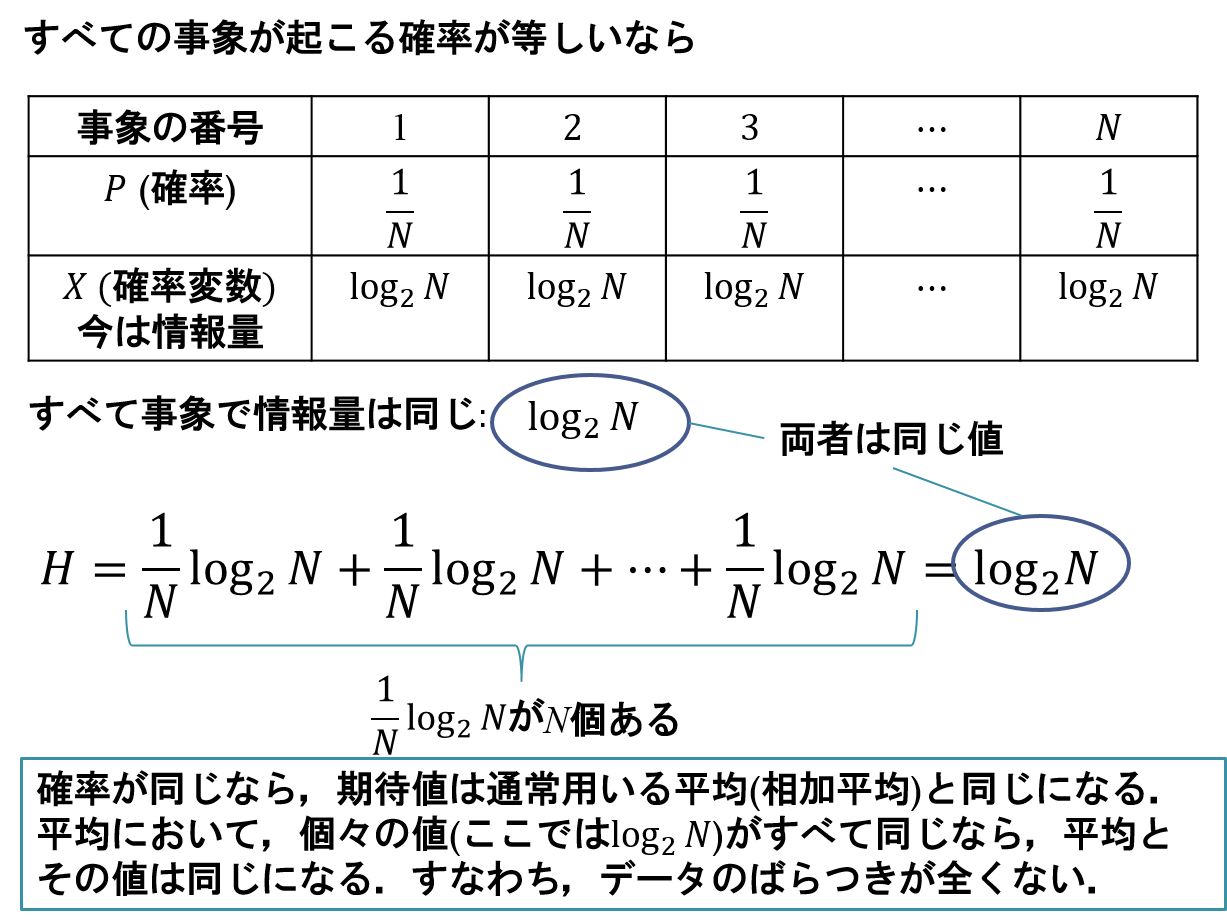
最初に、すべての事象が等確率で起こるものとする。このとき、事象の数の対数を情報量といい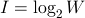 (bit)で表す。ここで、Wは事象の数である。使用できる文字が1,0の2つだけなので、logの底は2である。Wが2のべき乗で表現される場合、情報量は以下のように簡単に計算できる。
(bit)で表す。ここで、Wは事象の数である。使用できる文字が1,0の2つだけなので、logの底は2である。Wが2のべき乗で表現される場合、情報量は以下のように簡単に計算できる。
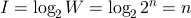 (bit)
(bit)
| 事象の数(W) | 2のべき乗(2n) | ビット(I) |
| 2 | 21 | 1 |
| 256 | 28 | 8 |
| 65536 | 216 | 16 |
nビットとは、0、1で表現された数が、n桁であることを意味する。
例として、いくつかの文字コードのビット数を表す。
| ASCIIコード(英語) 7ビット シフトJIS(日本語) 16ビット |
シフトJISがASCIIコードよりもビット数が大きいのは、日本語が英語に比べ文字数が多いためである。
次に情報を得るということを単純化して考える。取りうる事象の数が
Wであったものが、情報を得ることで、W'、W"と絞られ、最終的には1になる
ことを考える。例えばさいころの目を例としてあげる。
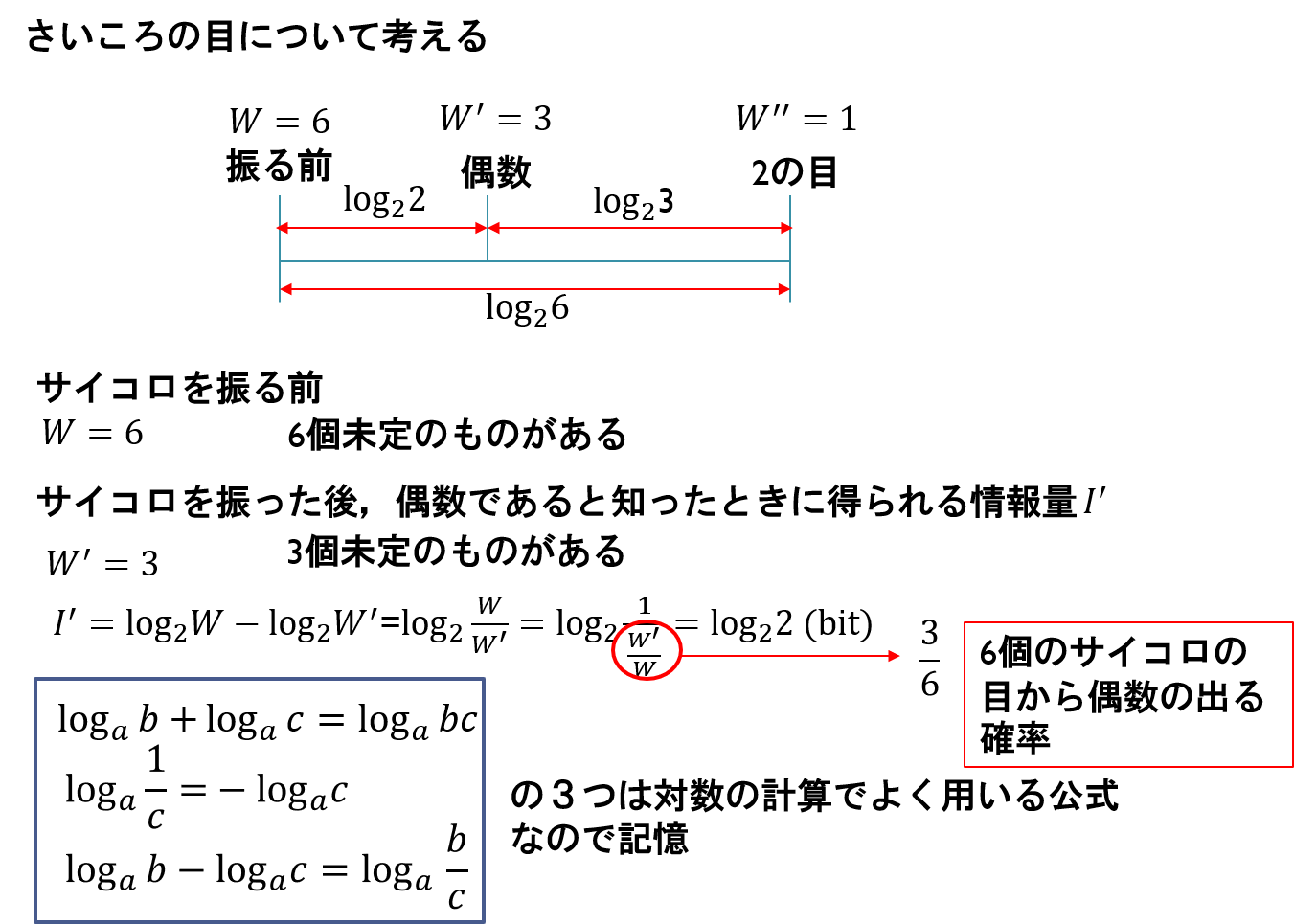
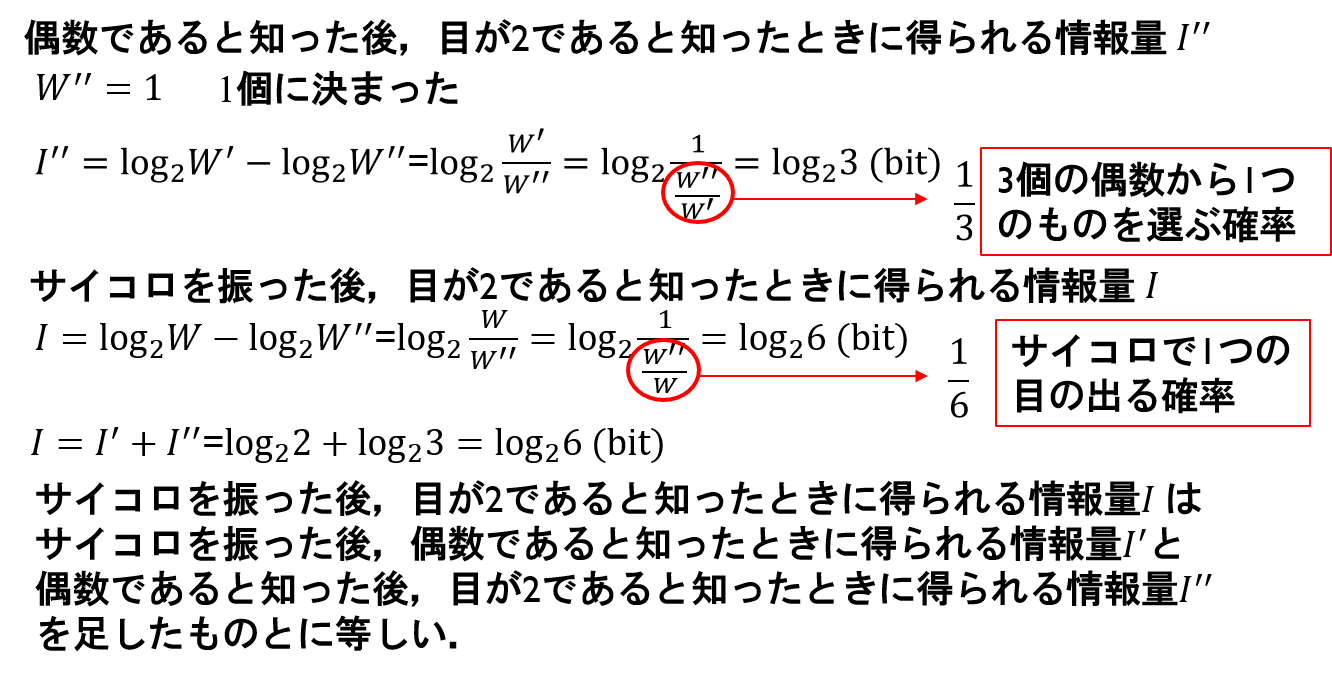
一般に、事象はそれぞれ起こる確率が異なる。そのため、i番目の事象の情報量は、その事象の確率を含む次式で表される。
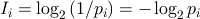 (bit)
(bit)すなわち、めったに起こらない事象が起こった場合、情報量は大きくなる。
1.1.3 情報エントロピー
情報エントロピーは、情報量の期待値として次式で表される。
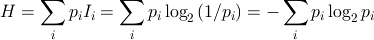 (bit)
(bit)
ここで、iは事象の番号であり、∑はすべての事象について和をとることを示す。情報エントロピーは平均情報量とも呼ばれる。
例として、表と裏の出る確率が半々のコインがもつ情報エントロピーを計算してみる。今、i=1を表が出る事象、i=2を裏が出る事象とする。p1=1/2 p2=1/2なので
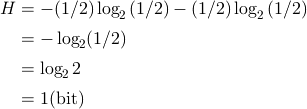
同様に絶対に表しかでないコインが持つ情報エントロピーを計算してみる。
p1=1
p2=0なので
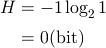
2事象のエントロピーのグラフは、次のようになる。
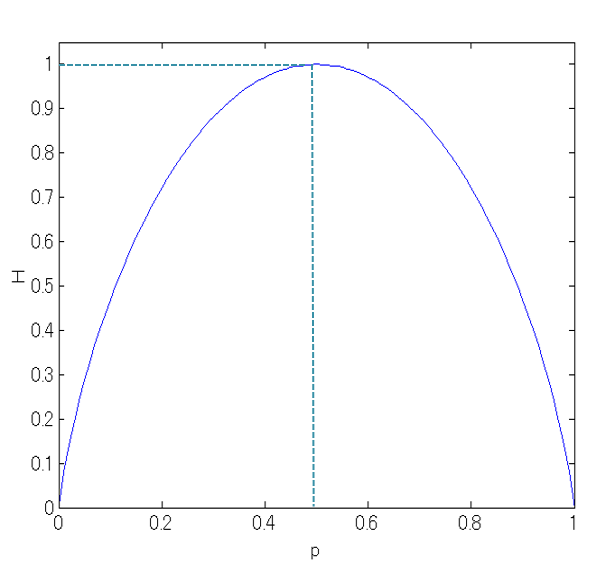 図2
図2 

1.2 メディア
メディアは媒介、媒体を意味する。情報を保管する媒体としてだけでなく、情報を伝達する媒体の意味もある。
1.3 情報メディア
情報メディアとは、文字・音声・画像・動画などの形にされた情報を保管したり、伝達したりする媒体のことを言う(図3)。特にコンピュータでは、情報は2進数で表現される。情報メディアには、情報を一方向に伝達する放送系メディアであるテレビやラジオ、また、情報を双方向で伝達することが可能な通信系メディアである電話やインターネット、また、情報を蓄積するパッケージ系メディアである書籍、フロッピーディスク、CD-ROMなど様々なものがある。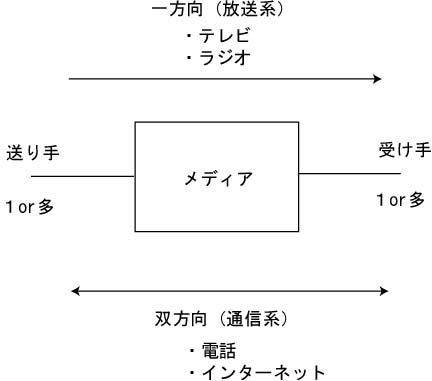 図3
図3課題.1
|
(1) ypuをASCII コード(7 ビット)で表現する。文字と文字の間はスペースを空ける。
また、それを16進数に書き直す。 (2)サイコロの目で、1が1/2, 2が1/4, 3が1/16, 4が1/16, 5が1/16, 6が1/16の確率で出現するときの情報エントロピーを求める。 |